TS model selection and validation
Built with
Page icon

TS model selection and validation

Risk, empirical risk, generalization and fitting strategies

Called x∈Xx \in \mathcal{X}  out inputs, y∈Yy \in \mathcal{Y}  our target, and P(X,Y)\mathbb{P}_{(X, Y)} their true joint distribution.
If we define fA(D):X→Yf_{\mathcal{A}(D)}: \mathcal{X} \rightarrow \mathcal{Y} as a forecasting model learned by a learning algorithm A\mathcal{A} on adaset D:=(xi,yi)i=1N\mathcal{D} := {(x_i, y_i)_{i=1}^N},
model selection is driven by our will to minimize the risk, defined by a loss function L(f(x),y)\mathcal{L}(f(x),y):
R=R[fA(D)]=Ex,y∼P(X,Y)[L(f(x),y)]\begin{align} \mathcal{R}=& \mathcal{R}[f_{\mathcal{A}(\mathcal{D})}]\\ =&\mathbb{E}_{x, y \sim \mathbb{P}_{(X, Y)}}[\mathcal{L}(f(x), y)] \end{align}
However, since the true join distribution P(X,Y)\mathbb{P}_{(X, Y)} is unknown, the training process usually involves minimizing the empirical risk on D\mathcal{D}:
RD=RD[fA(D)]=EDL(f(x),y)=∑i∈DL(f(xi),yi)\begin{align} \mathcal{R}_{\mathcal{D}} =& \mathcal{R}_{\mathcal{D}}[f_{\mathcal{A}(\mathcal{D})}]\\ =&\mathbb{E}_{\mathcal{D}}\mathcal{L}\left(f\left(x\right), y\right)\\ =& \sum_{i \in \mathcal{D}} \mathcal{L}\left(f\left(x_i\right), y_i\right) \end{align}

❓ Why minimizing the empirical risk alone is not a good criteria for model selection?

Model selection, generalization error, overfitting

We can state the task of model selection using three slightly different concepts:
Minimize the out of sample risk
RD~[f]=∑i∈D~L(f(xi),yi)\mathcal{R}_{\mathcal{\tilde{D}}}[f]=\sum_{i \in \mathcal{\tilde{D}}} \mathcal{L}\left(f\left(x_i\right), y_i\right)
where D~\tilde{D}  is a new dataset, unobserved during training.
Minimize RD\mathcal{R}_{\mathcal{D}}  and the generalization gap
If we are not directly interested in the performance of a model, but rather, how it could degrade on unseen data, we are interested in its generalization gap:
R−RD∼RD~−RD\mathcal{R} -\mathcal{R}_{\mathcal{D}} \sim \mathcal{R}_{\mathcal{\tilde{D}}} -\mathcal{R}_{\mathcal{D}} 
Minimize RD\mathcal{R}_{\mathcal{D}}  while limiting overfitting
The dual notion of small generalization error is overfitting:
minimizing overfitting risk increase generalization
if a model is overfitted, the generalization on new data will be poor

Information based criteria

A way to control overfitting, and thus selecting a model with better generalization, is to directly punish the model complexity:
f(θ∗)=arg min⁡f∈fA(D)RD(θ)+λC(θ)f(\theta^*) = \argmin_{f\in f_{\mathcal{A}(D)}} \mathcal{R}_{\mathcal{D}}(\theta) + \lambda C(\theta)
If the model has a known predictive (generative) distribution, under iid assumption the empirical risk is replaced by the sum of empirical log-likelihood ℓ(θ)=1N∑i∈Dlog⁡p(y∣θ)\ell(\theta) = \frac{1}{N} \sum_{i\in \mathcal{D}}\log p(y\vert \theta), and the complexity measure is replaced by C(θ)=−log⁡π0(θ)C(\theta)=-\log \pi_0(\theta), where π0(θ)\pi_0(\theta)  is some prior distribution, we obtain the MAP estimate:
f(θ∗)=arg max⁡f∈fA(D)ℓ(θ)+log⁡π0(θ)\begin{equation} f(\theta^*) = \argmax_{f\in f_{\mathcal{A}(D)}} \ell(\theta) + \log\pi_0 (\theta) \end{equation}
Under the information theory lens, this method for controlling overfitting can be seen as the more convenient way to communicate data D\mathcal{D} to a receiver. This task can be splitted in:
communicate a model: this takes −log⁡π(θ)-\log \pi(\theta)  bits
to perfectly know the data, we need to additionally communicate the reconstruction error, which takes 1N∑i∈Dlog⁡p(y∣θ)=ℓ(θ)\frac{1}{N} \sum_{i\in \mathcal{D}}\log p(y\vert \theta) = \ell(\theta)

BIC and AIC

Bayesian information criterion and Akaike information criterion have the same form of (6). While BIC can be derived from an approximation of the marginal likelihood of a model, AIC can be derived from a frequentist perspective. Their forms are:
BIC
−2log⁡p(D∣θ^,m)+Dmlog⁡N-2 \log p(\mathcal{D} \mid \hat{\theta}, m)+D_m \log N
AIC
−2log⁡p(D∣θ^,m)+2Dm-2 \log p(\mathcal{D} \mid \hat{\theta}, m)+2 D_m
penalizes complex models less heavily than BIC (no dependence on N)
only valid for relative comparisons
only handy for models with limited degrees of freedom, not much for non-parametric models.

Cross validation

In a data-rich situation the best is to split the dataset in training and test.
However, we can usually assume to be in a data-scarce regime
We partition the data D\mathcal{D} into kk sets or folds: D1,D2…Dk\mathcal{D}_1, \mathcal{D}_2 \dots \mathcal{D}_k​
We train the model m on D−i=[Dj]j≠i\mathcal{D}_{-i} = [\mathcal{D}_j]_{j\neq i} and test it on Di\mathcal{D}_i, retrieving RDi\mathcal{R}_{\mathcal{D}_i}​
We average the empirical out of sample risk RDi\mathcal{R}_{D_i}  over the different folds
This process leads to the estimation of the expected (over training and testing sets) out of sample error: ED∈DiRDi\mathbb{E}_{ \mathcal{D}\in\mathcal{D}_i}\mathcal{R}_{\mathcal{D}_i} , which is not the error we should expect from the final fitted model.
it is an estimation of the average prediction error of the model fit on other unseen data from the same population
this estimation could however be conservative, since each data point is used for both training and testing several times
iid could not be respected for future data
However, since these conditions hold for all the models that we test, CV is empirically a good method to perform model selection

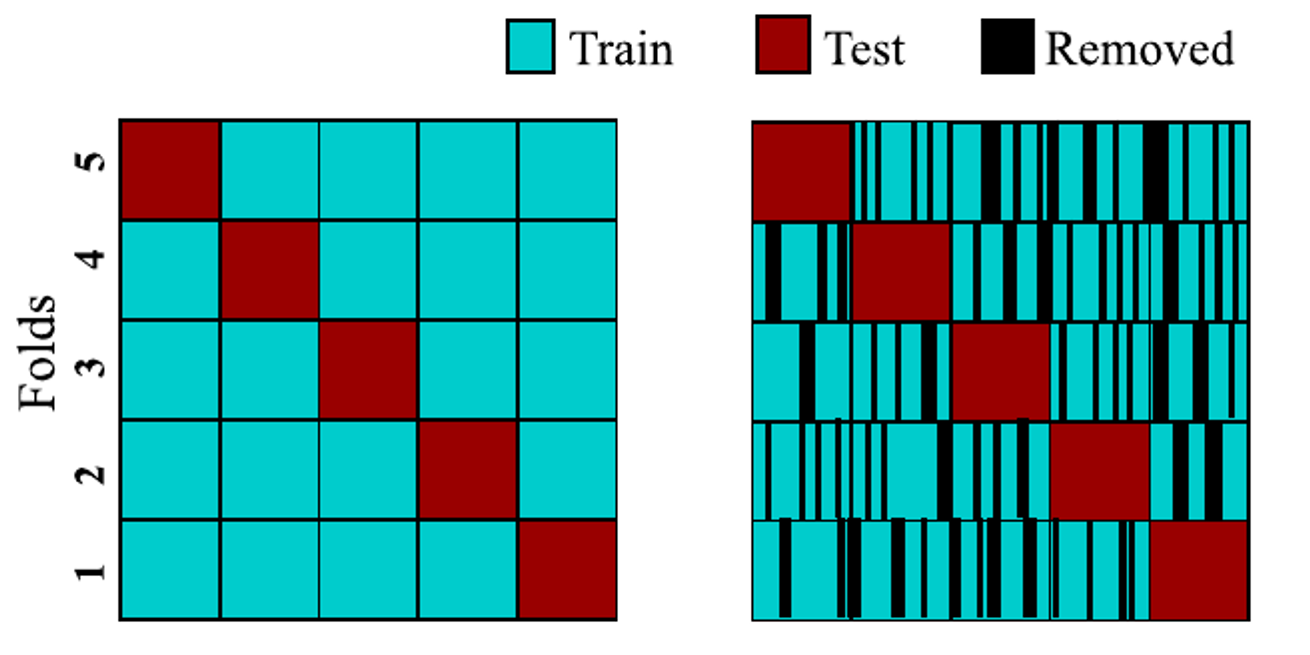
K-folds CV

Standard k-folds:
random shuffle
evenly spaced folds
possibly observations highly correlated with the test set are removed
ALT

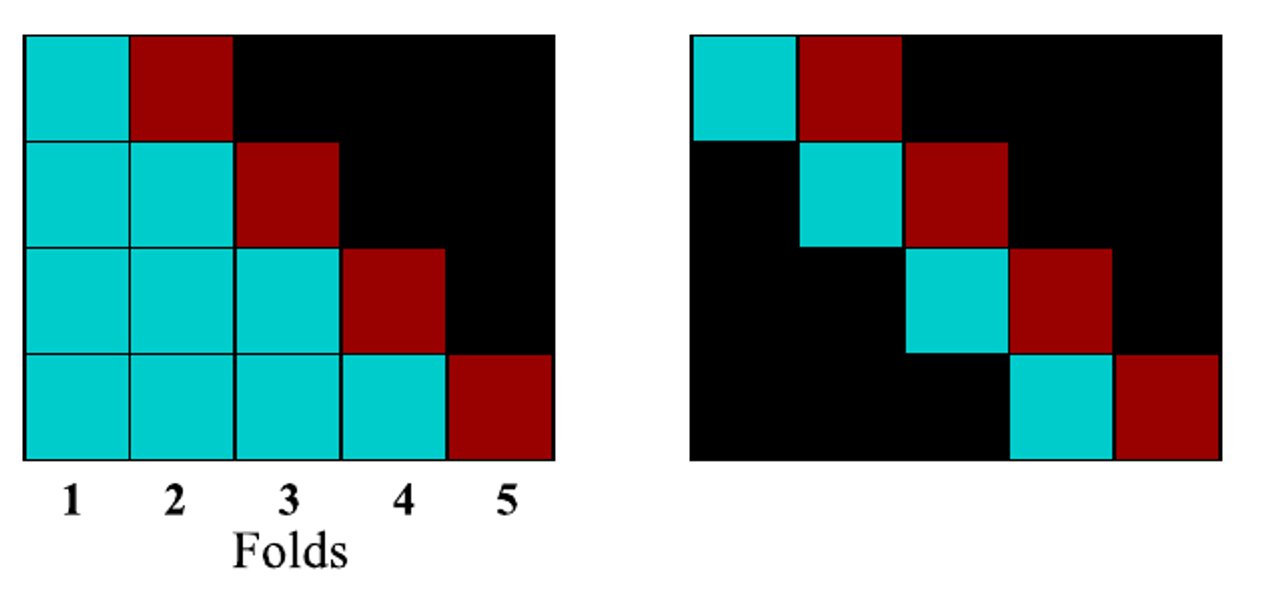
Prequential (TS CV)

Since time series inherently deal with causality (past data has an effect on future data), the earliest and simplest time-series CV simply builds sets of increasing lengths (b). However:
the earliest fold is completely unrepresented. Earliest folds are trained on limited amount of data.
If hyperparameters are tuned, the selected ones are unlikely to work well on the full dataset
last folds are over-represented
To overcome these issues, sliding window approaches can be used, in which the test is done on a sliding window.
However, this approach is still not suited for data-driven models requiring high quantity of data.
ALT
Left: classical TS-CV. RIght: sliding window approach
ALT

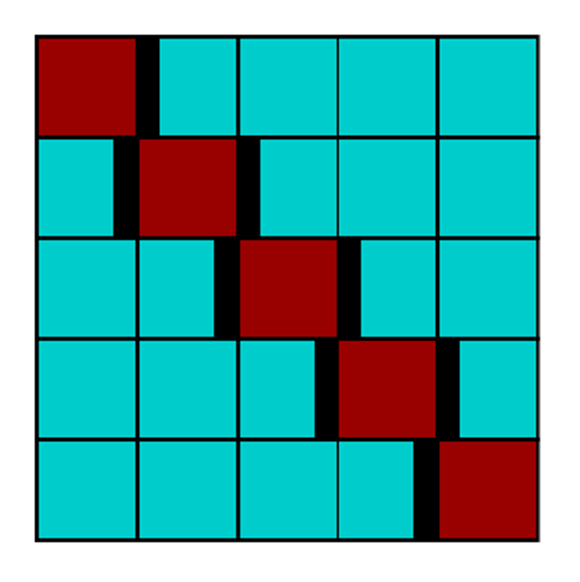
Purged approaches

💡
The solution to this challenge is to realize that the future can, in many cases, actually be used to forecast the past, if we limit the data on each series appropriately. The model and selected hyperparameters gain the benefit of a full and robust training set, while each data point remains aware of only its own past results. The key insight is to purge or embargo some data between each fold, sufficient to cover the longest forecasting interval and any excess amount needed to prevent any short- term trends appearing across multiple folds - A.D.Lainder, R.D. Wolfinger, Forecasting with gradient boosted trees: augmentation, tuning, and cross-validation strategies Winning solution to the M5 Uncertainty competition, 2022
ALT
Data is not shuffled
Pairs of highly correlated data are removed
If data is using p past observations from the signal to predict n steps ahead, a good rule of thumb is to use p+n as embargo period

❓ What happens if the best performing model out of the k folds is used as final forecaster?

Statistics for time-series model selection

Diebold-Mariano test

The Diebold-Mariano test is a statistical test used for comparing the accuracy of two sets of forecasts, at a given step ahead. The test compares the forecast errors for each set of forecasts and determines whether one set of forecasts is significantly more accurate than the other.
Defined d as the difference of the losses between two forecasters:
d=l(y,y^1)−l(y,y^2)d = l(y, \hat{y}_1)-l(y, \hat{y}_2)
The Diebold-Mariano statistics is given by:
DM=dˉ[γ0+2∑k=1h−1γk]/nD M=\frac{\bar{d}}{\sqrt{\left[\gamma_0+2 \sum_{k=1}^{h-1} \gamma_k\right] / n}}
Where γk=1n∑i=k+1n(di−dˉ)(di−k−dˉ)\gamma_k=\frac{1}{n} \sum_{i=k+1}^n\left(d_i-\bar{d}\right)\left(d_{i-k}-\bar{d}\right) is the correlation at lag k of dd.
Under the assumption that there’s no difference between the two forecasts, we have that DM follows a Normal distribution:
DM∼N(0,1)D M \sim N(0,1)
The null hypothesis of no differences will be rejected if the DM statistics falls outside the ∣DM∣>zα/2|D M|>z_{\alpha / 2} range.

Small sample correction

For small sample sizes, DM test tends to reject the null hypothesis too often for small samples. A better test is the Harvey, Leybourne, and Newbold (HLN) test, which is based on the following:
HLN=DM[n+1−2h+h(h−1)]/n∼T(n−1)H L N=D M \sqrt{[n+1-2 h+h(h-1)] / n} \sim T(n-1)
The Nemenyi test is a post-hoc pairwise test, which is used to compare a set of m different models on a group of n independent experiments.
Usually performed after a Friedman’s test, which is a non-parametric analog of variance for a randomized block design. This test if there’s a difference in a set of n forecasters
a matrix R∈RN×kR \in \mathbb{R}^{N \times k} whose elements ri,jr_{i, j} are the ranks for experiment i and model j, is obtained.
The mean rank for each model is retrieved through column-wise averages of RR.
Friedman’s test for k algorithms on N datasets is used to see if there’s a difference between the k forecasters
12Nk(k+1)[∑jRj2−k(k+1)24]∼χF2\frac{12 N}{k(k+1)}\left[\sum_j R_j^2-\frac{k(k+1)^2}{4}\right]\sim \chi_F^2
The performance of two models is identified as significantly different by the Nemenyi test if the corresponding average ranks differ by at least the critical difference: CD=qα,NN(N+1)12kC D=q_{\alpha, N} \sqrt{\frac{N(N+1)}{12 k}}​
where qαq_{\alpha} is the quantile α of the Studentized range statistic with N samples.
You can find an implementation of Nemenyi test for python in the scikit-posthocs library.