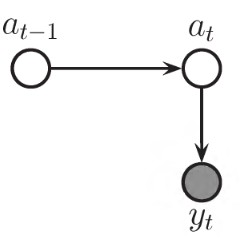
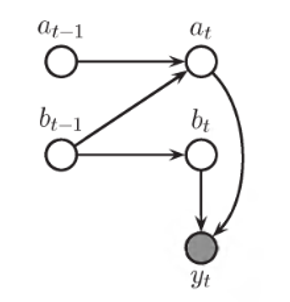
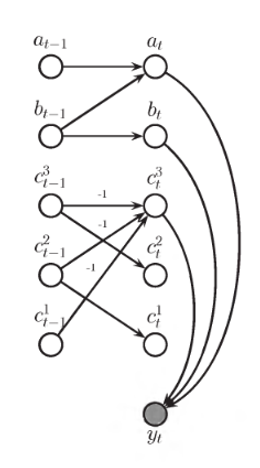
State Space models for forecasting
Built with
Page icon

State Space models for forecasting

State space models, a brief introduction

State space models (sometimes known as latent variable models) are equivalent to HMMs
system equationxt=f(xt−1,ut−1,εt)measurement equationyt=g(xt−1,ut−1,δt) \begin{aligned}\text{system equation} \qquad x_t &= f(x_{t-1}, u_{t-1}, \varepsilon_t)\\[1em] \text{measurement equation} \qquad y_t &= g(x_{t-1}, u_{t-1}, \delta_t)\end{aligned}
Assumptions:
markovian property
zero mean, iid Gaussian noise: εt∼N(0,Qt),δt∼N(0,Rt),εt⊥δt\varepsilon_t\sim \mathcal{N}(0, Q_t), \quad \delta_t\sim \mathcal{N}(0, R_t), \quad \varepsilon_t \perp \delta_t​
Additionally, we just consider stationary models, that is, parameters of f,gf, g are considered constant in time.
Applications:
Object tracking
Process modeling
Optimization
System identification and modeling
Forecasting
Exponential smoothing
ARMA / Box Jenkins
ARIMAX
All these applications have developed slightly different notations and consider slightly different terms and assumptions.
We will review them under a general framework / notation, from which all of them can be derived.

Linear, time invariant models

We will restrict the explanation to linear models, but all the explained properties hold also for non-linear models. Moreover, we will assume that the parameters of the model are fixed in time.
Process form - Multiple source of errors
xt=Axt−1+But−1+εtyt=Cxt−1+Dut−1+δt\begin{aligned}x_t & =A x_{t-1}+B u_{t-1}+\varepsilon_t \\y_t & =C x_{t-1}+D u_{t-1}+\delta_t\end{aligned}
→ Kalman filter gain K →
Innovation form - Single source of error
xt=Axt−1+But−1+Kεtyt=Cxt−1+Dut−1+εt\begin{aligned}x_t & =A x_{t-1}+B u_{t-1}+K \varepsilon_t \\y_t & =C x_{t-1}+D u_{t-1}+\varepsilon_t\end{aligned}
All the tractation of exponential models for forecasting assumes an innovation form. We briefly review the Kalman filter theory which must be used to pass from process to innovation form.

Kalman filter

The Kalman filter is one of the most important and common estimation algorithms. It performs an exact Bayesian filtering for linear-Gaussian state space models. It can be used to:
estimate hidden (unknown) states based on a series of (noisy) measurements. Ex: GPS location and velocity = hidden states, differential time of the satellites' signals' arrival = measurements. Ex2: trajectory estimation for the Apollo program.
ALT
predict / forecast future system’s state based on past estimations. Ex: nowcasting
ALT

Example: tracking positions

Suppose we want to track the position of a robot in the woods, having just the readings of a unreliable GPS tracker.
x=[pv]x = \left[ \begin{align*}p\\v\end{align*} \right]
We can write a useful state space model for the tracking using our knowledge on the laws of motion:
pt=pt−1+vt−1Δt+12at−1Δt2vt=vt−1+at−1Δt\begin{aligned}p_t & =p_{t-1}+v_{t-1} \Delta t+\frac{1}{2} a_{t-1} \Delta t^2 \\v_t & =v_{t-1}+a_{t-1} \Delta t\end{aligned}
…write the balance equations in matrix form
xt=[1Δt01]⏟Axt−1+[12Δt2Δt]⏟Bat−1x_t=\underbrace{\left[\begin{array}{cc}1 & \Delta t \\0 & 1\end{array}\right]}_A x_{t-1}+\underbrace{\left[\begin{array}{c} \frac{1}{2}\Delta t^2 \\\Delta t\end{array}\right]}_B a_{t-1}
…and obtain the stochastic formulation
xt=Axt−1+But−1+εtyt=Cxt−1+δtεt∼N(0,Qt),δt∼N(0,Rt)εt⊥δt\begin{aligned}x_t & =A x_{t-1}+B u_{t-1}+\varepsilon_t \\y_t & =C x_{t-1}+\delta_t\\ \varepsilon_t&\sim \mathcal{N}(0, Q_t), \quad \delta_t\sim \mathcal{N}(0, R_t) \\ \varepsilon_t &\perp \delta_t \end{aligned}

Uncertainty propagation for linear-Gaussian variables

The zero-mean Gaussian distribution is completely determined by its covariance matrix Σ:12π∣Σ∣e∥x∥Σ−1\Sigma: \frac{1}{\sqrt{2\pi}\vert\Sigma\vert} e^{\Vert x\Vert\Sigma^{-1}}​
If the variable xx has a Gaussian distribution x∼N(μx,Σx)x \sim \mathcal{N}(\mu_x, \Sigma_x), so it has its linear transformation. You can view the linear operator AxAx  as a superposition of two linear transformations: one on the mean value of x,μxx, \mu_x, which can be treated as deterministic, and one on an associated zero-mean error distributed as N(0,Σ)\mathcal{N(0, \Sigma)}:
Ax=Aμx+N(0,AΣAT)Ax = A\mu_x + \mathcal{N}(0, A\Sigma A^T)
Why is the covariance of the Gaussian rescaled in this way? From the definition of covariance:
Cov(Ax)=∑t(Axt−Axˉ)(Axt−Axˉ)T=∑tA(xt−xˉ)(xt−xˉ)TAT=A∑t(xt−xˉ)(xt−xˉ)TAT=ACov(x)AT\begin{align} Cov(Ax)&=\sum_t (Ax_t-A\bar{x})(Ax_t-A\bar{x})^T\\ &= \sum_t A(x_t-\bar{x})(x_t-\bar{x})^TA^T\\ &= A\sum_t (x_t-\bar{x})(x_t-\bar{x})^TA^T = A Cov(x)A^T \end{align}

Uncertainty propagation

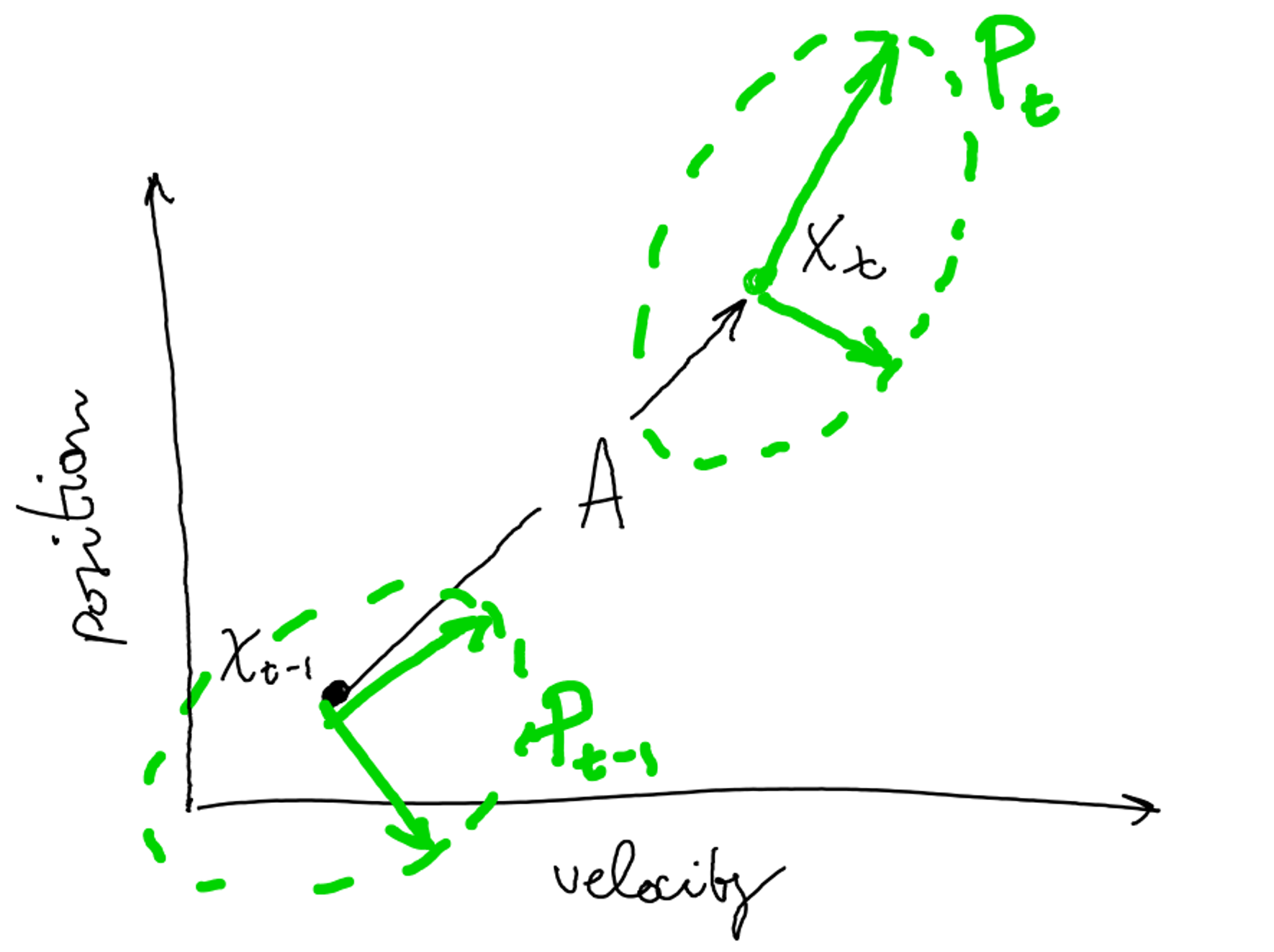
In general, to improve the state estimation, it is useful to know if states are correlated. In this case, the robot could have higher velocities at particular positions (e.g. on a slope). Let’s assume the states have a Gaussian distribution Nx(x,P)\mathcal{N}_x(x, P) where P∈S2P\in \mathbb{S}^2 is the (symmetric) states’ covariance matrix.
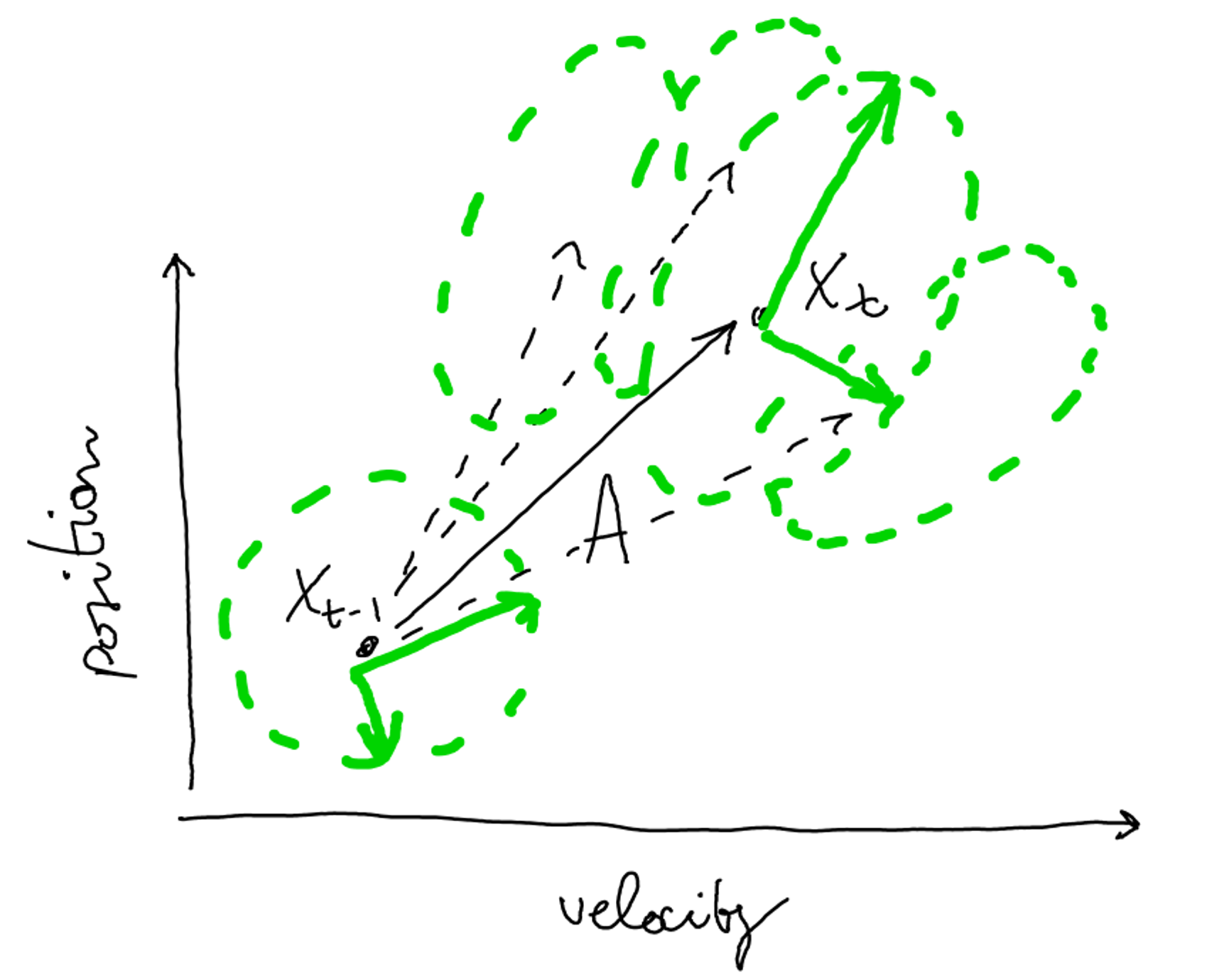
How the state’s uncertainty spreads through time?
Deterministic step: shift
CoV(xt−1)=Pt−1CoV(xt)=CoV(Axt−1)=APt−1AT=PtCoV(x_{t-1}) = P_{t-1}\\ CoV(x_{t}) = CoV(Ax_{t-1}) = AP_{t-1}A^T = P_t​
ALT
State uncertainty prediction for next step t, given the state covariance at time t-1
ALT
System noise: Gaussian blob→ still Gaussian
Pt=APt−1A⊤+Qtxt∼Nx(Axt−1,Pt)P_t=A P_{t-1} A^{\top}+Q_t\\ x_t \sim \mathcal{N}_x(A x_{t-1}, P_t)​
ALT
Additional uncertainty given by the system noise, affecting the next state’s prediction
ALT
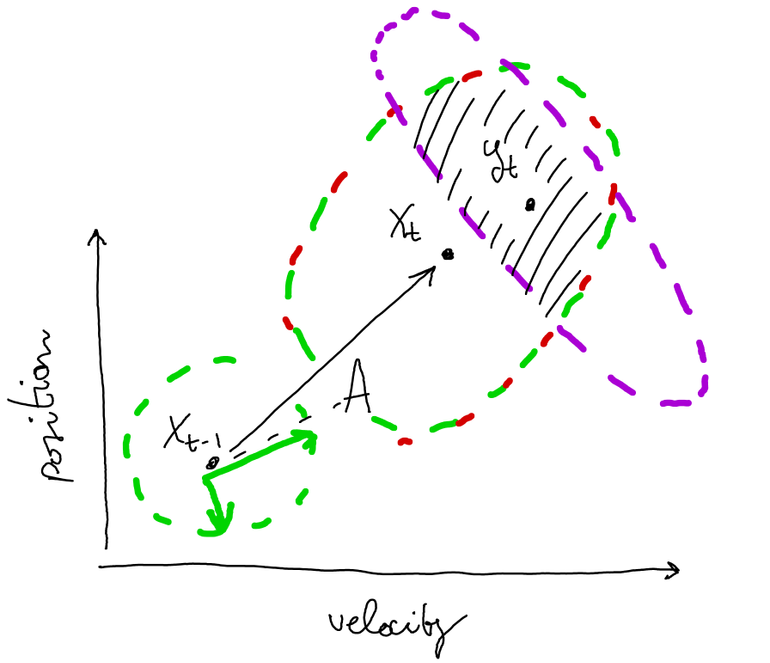
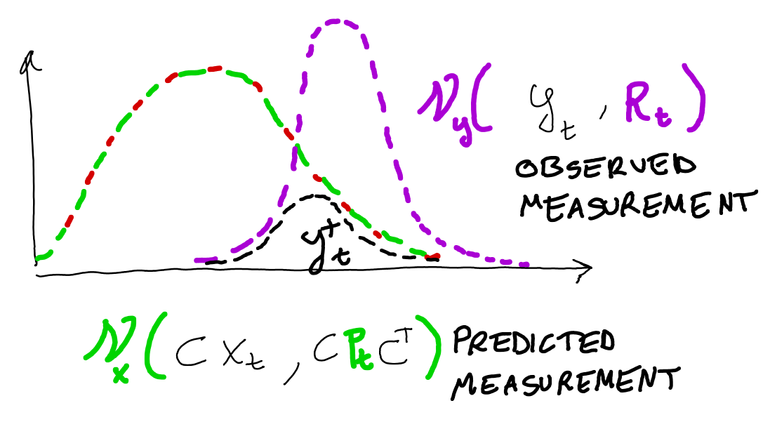
Exploit sensor’s observations:
predicted measurement yt∣xt∼Nxy(Cxt,CPtCT)y_{t\vert x_t} \sim \mathcal{N}_{xy}(Cx_t, CP_tC^T)​
observed measurement yt∼Ny(yt,Rt) y_t \sim \mathcal{N}_y(y_t, R_t)​
ALT
The uncertainty on the prediction can be reduced when we observe a new output from the GPS
ALT

Derivation of Kalman gain

The dashed space in the last picture shows the region where is most probable to find the state at time t, given the observations from the sensor. How does the predicted and observed measurements Nxy,Ny\mathcal{N}_{xy}, \mathcal{N}_y combine? Since we said that εt⊥δt\varepsilon_t \perp \delta_t :
P(yt+∣xt,yt)=P(yt)⋅P(yt∣xt)=Ny(yt,R)Nxy(Cxt,CPtCT)\begin{aligned} P\left(y^+_t \mid x_t, y_t\right)&=P\left(y_t\right) \cdot P\left(y_{t\vert x_t}\right)\\ &=\mathcal{N}_y(y_t, R)\mathcal{N}_{xy}(Cx_t, CP_tC^T)\end{aligned}​
The multiplication of two univariate gaussians leads to:
μ+=μ0+σ02(μ1−μ0)σ02+σ12=μ0+K(μ1−μ0)σ+=σ0−σ04σ02+σ12=σ02−kσ02\begin{aligned}& \mu^{+}=\mu^0+\frac{\sigma_0^2\left(\mu_1-\mu_0\right)}{\sigma_0^2+\sigma_1^2}=\mu_0+K\left(\mu_1-\mu_0\right) \\& \sigma^{+}=\sigma_0-\frac{\sigma_0^4}{\sigma_0^2+\sigma_1^2}=\sigma_0^2-k \sigma_0^2\end{aligned}
We can then write
yt+=Cxt+K(yt−Cxt)y_t^{+}=C x_t+K\left(y_t-C x_t\right)​
Interpretation: we are linearly correcting the measurement with the sensor’s values, with a weight proportional to the uncertainty on the predicted measure.
ALT
The covariance update can be written as:
Ry+=Pt(I−K)K=CPtCT(CPtCT+Rt)−1\begin{align}R_y^+ &= P_t(I-K)\\ K &= CP_tC^T(CP_tC^T+R_t)^{-1} \end{align}

Linear state space model estimation

xt=Axt−1+But−1+Kεtyt=Cxt−1+Dut−1+εt\begin{align}x_t & =A x_{t-1}+B u_{t-1}+K \varepsilon_t \\y_t & =C x_{t-1}+D u_{t-1}+\varepsilon_t\end{align}
❓ How can we estimate A, B, C, D, if we don’t observe state x?
Noise elimination
Since in the innovation form the noise εt\varepsilon_t enters both the equations at time t, we can eliminate one equation by substituting εt=yt−Cxt−1+Dut−1\varepsilon_t = y_t - Cx_{t-1} + Du_{t-1} back in the first equation:
x1=Ax0+Bu0+K(ε0)=Ax0+Bu0+K(y1−Cx0+Du0)=(A−KC)x0+(B−KD)u0+Ky1=A~x0+B~u0+Ky1\begin{align} x_1 &= A x_0 + Bu_0 + K(\varepsilon_0) \\ &= A x_0 + Bu_0 + K(y_1 - Cx_0 + Du_{0})\\ &= (A -KC)x_0 + (B-KD)u_0 + Ky_1\\ &=\tilde{A}x_0+ \tilde{B}u_0 + Ky_1 \end{align}
State elimination
We can now recursively find the state at the next step as an expression of previous inputs and observations:
start with x1=A~x0+B~u0+Ky1x_1 = \tilde{A}x_0+ \tilde{B}u_0 + Ky_1​
explicit next state as x2=A~x1+B~u1+Ky2=A~(A~x0+B~u0+Ky1)+B~u1+Ky2x_2 = \tilde{A}x_1+ \tilde{B}u_1 + Ky_2 = \tilde{A}(\tilde{A}x_0+ \tilde{B}u_0 + Ky_1 )+ \tilde{B}u_1 + Ky_2 ​
repeat iteratively
By recursive substitution, we get:
[x0x1⋮⋮xT]=[IA~⋮⋮A~T]x0+[0⋯⋯010⋯0A~1⋯0⋮⋱⋱0A~T−1⋯A~1][B~u0+Ky0B~u1+Ky1⋮⋮B~uT−1+KyT−1]\left[\begin{array}{c}x_0 \\x_1 \\\vdots \\\vdots \\x_T\end{array}\right]=\left[\begin{array}{c}I \\\tilde{A} \\\vdots \\\vdots \\ \tilde{A}^T\end{array}\right] x_0+\left[\begin{array}{cccc}0 & \cdots & \cdots & 0 \\ 1& 0 & \cdots & 0 \\ \tilde{A} & 1 & \cdots & 0 \\\vdots & \ddots & \ddots & 0 \\ \tilde{A}^{T-1} & \cdots & \tilde{A} & 1\end{array}\right]\left[\begin{array}{c}\tilde{B}u_0 + Ky_0\\ \tilde{B}u_1+ Ky_1 \\\vdots \\\vdots \\ \tilde{B}u_{T-1}+ Ky_{T-1}\end{array}\right]
We can see that at each step tt, the new state is a function of the initial state x0x_0 and a weighted sum of past inputs uu and observations yy.
If we now use the state at time TT  as input to predict the new observation yT+1y_{T+1}, we get:
y^T+1=A~Tx0+∑t=0TA~t(B~ut+Kyt)=at+∑t=0Tctyt+btut\hat{y}_{T+1} = \tilde{A}^Tx_0 + \sum_{t=0}^T\tilde{A}^t(\tilde{B}u_t + Ky_t) = a_t + \sum_{t=0}^Tc_ty_t + b_tu_t
This means that the forecasts of a state-space model in innovation form can be reformulated as a weighted sum of past observations and inputs. This form is also called the reduced form of the model.
This form show that ARIMA models can be formulated as SS models. Also exponential smoothing models can be formulated as SS, as we see in the following

Exponential smoothing

y=T+S+Ey=T+S+E

Trend component - simple exponential smoothing (T)

The simplest exponential smoothing just models the trend as a weighted sum between the last prediction and the last observation
y^t+1=αyt+(1−α)y^t\hat{y}_{t+1}=\alpha y_t+(1-\alpha) \hat{y}_t
By recursive substitution, this becomes:
y^t+1=αyt+(1−α)y^t=αyt+(1−α)(αyt−1+(1−α)y^´t−1)=…=∑k=0Tα(1−α)kyt−k\hat{y}_{t+1} = \alpha y_t+(1-\alpha) \hat{y}_t = \alpha y_t + (1-\alpha)(\alpha y_{t-1} + (1-\alpha)\hat{y}_{´t-1})= \dots\\ =\sum_{k=0}^{T}\alpha (1-\alpha)^ky_{t-k}
…which represents a weighted moving average of all past observations with the weights decreasing exponentially, which smooths the observations
There are various methods that fall into the exponential smoothing family. Each has the property that forecasts are weighted combinations of past observations, with recent observations given relatively more weight than older observations. All share the name “exponential smoothing,” reflecting the fact that the weights decrease exponentially as the observations age.

Equivalent representations

The component form gives the relations between the different model’s components. This is a procedural form, whose recursion gives the mean prediction. To pass from the component form to the state-space form, we must explicit the presence of measurement and process noise.
Component form
Forecast equationy^t+h∣t=ℓtSmoothing equationℓt=αyt+(1−α)ℓt−1\begin{align*}\text{Forecast equation} \quad &\hat{y}_{t+h \mid t}=\ell_t \\ \text{Smoothing equation} \quad &\ell_t=\alpha y_t+(1-\alpha) \ell_{t-1}\end{align*}
yt=y^t+εt=ℓt−1+εty_t = \hat{y}_t + \varepsilon_t = \ell_{t-1}+\varepsilon_t
State Space form
yt=[1]xt−1+εtxt=[1]xt−1+αεt\begin{aligned}& y_t=\left[1\right] x_{t-1}+\varepsilon_t \\& x_t=\left[1\right] x_{t-1}+\alpha \varepsilon_t\end{aligned}
ALT

Holt’s linear trend method (T)

Holt (1957) extended simple exponential smoothing to allow the forecasting of data with a trend.
Component form
Forecasty^t+h∣t=ℓt+hbtSmoothed Levelℓt=αyt+(1−α)(ℓt−1+bt−1)Smoothed Trendbt=β∗(ℓt−ℓt−1)+(1−β∗)bt−1\begin{align*}\text{Forecast} \quad &\hat{y}_{t+h \mid t}=\ell_t+h b_t \\ \text{Smoothed Level} \quad &\ell_t=\alpha y_t+(1-\alpha)\left(\ell_{t-1}+b_{t-1}\right)\\ \text{Smoothed Trend} \quad &b_t=\beta^*\left(\ell_t-\ell_{t-1}\right)+\left(1-\beta^*\right) b_{t-1}\end{align*}
State Space form
yt=[11]xt−1+εtxt=[1101]xt−1+[αβ]εt\begin{aligned}& y_t=\left[\begin{array}{ll}1 & 1\end{array}\right] \boldsymbol{x}_{t-1}+\varepsilon_t \\& \boldsymbol{x}_t=\left[\begin{array}{ll}1 & 1 \\0 & 1\end{array}\right] \boldsymbol{x}_{t-1}+\left[\begin{array}{l}\alpha \\\beta\end{array}\right] \varepsilon_t\end{aligned}
ALT
where ltl_t  denotes the estimation of the level, btb_t  represents the change of level (that is, the slope), always estimated with an exponential smoothing

Holt’s Winters method

The Holt’s Winters method incorporates a single seasonality effect.
y^t+h∣t=ℓt+hbt+st+h−m(k+1)ℓt=α(yt−st−m)+(1−α)(ℓt−1+bt−1)bt=β∗(ℓt−ℓt−1)+(1−β∗)bt−1st=γ(yt−ℓt−1−bt−1)+(1−γ)st−m,\begin{aligned}\hat{y}_{t+h \mid t} & =\ell_t+h b_t+s_{t+h-m(k+1)} \\\ell_t & =\alpha\left(y_t-s_{t-m}\right)+(1-\alpha)\left(\ell_{t-1}+b_{t-1}\right) \\b_t & =\beta^*\left(\ell_t-\ell_{t-1}\right)+\left(1-\beta^*\right) b_{t-1} \\s_t & =\gamma\left(y_t-\ell_{t-1}-b_{t-1}\right)+(1-\gamma) s_{t-m},\end{aligned}
ALT

… and many more

ALT

Estimation

Unlike linear regression, no closed form → numerical optimization must be used.
Parameters α,β,γ\alpha, \beta, \gamma are estimated maximising the likelihood.
For models with additive errors, equivalent to minimize the SSE
For models with multiplicative errors, not equivalent
yt=h(xt−1)⏟μt+k(xt−1)εt⏟etxt=f(xt−1)+g(xt−1)εt\begin{aligned}y_t & =\underbrace{h\left(\boldsymbol{x}_{t-1}\right)}_{\mu_t}+\underbrace{k\left(\boldsymbol{x}_{t-1}\right) \varepsilon_t}_{e_t} \\\boldsymbol{x}_t & =f\left(\boldsymbol{x}_{t-1}\right)+g\left(\boldsymbol{x}_{t-1}\right) \varepsilon_t\end{aligned}
Additive errorsk(x)=1.yt=μt+εtMultiplicative errorsk(xt−1)=μt.yt=μt(1+εt)εt=(yt−μt)/μt is relative error. \begin{aligned}\text{Additive errors}\\ k(x)&=1 . \quad y_t=\mu_t+\varepsilon_t\\ \text{Multiplicative errors}&\\ &k\left(\boldsymbol{x}_{t-1}\right)=\mu_t . \quad y_t=\mu_t\left(1+\varepsilon_t\right) \\& \varepsilon_t=\left(y_t-\mu_t\right) / \mu_t \quad \text { is relative error. }\end{aligned}
L∗(θ,x0)=Tlog⁡(∑t=1Tεt2)+2∑t=1Tlog⁡∣k(xt−1)∣=−2log⁡( Likelihood )+ constant \begin{aligned}L^*\left(\boldsymbol{\theta}, \mathbf{x}_0\right) & =T \log \left(\sum_{t=1}^T \varepsilon_t^2\right)+2 \sum_{t=1}^T \log \left|k\left(\mathbf{x}_{t-1}\right)\right| \\& =-2 \log (\text { Likelihood })+\text { constant }\end{aligned}